统计光谱学概要

当我们采取光谱学测量时，我们预计结果可以准确和精确。但是，准确和精确取决于许多因素，在现实世界中，每次测量都会包括错误的余量。实际上，我们从光谱学测量中获得的结果不完整，除非我们包括错误，即组成的平均值为20％，误差距+/- 0.2％。

误差范围是由于测量系统中的随机变化，并遵循统计规律。学习这些规则以及如何应用它们是为我们自己估计误差范围的第一步光谱测量．

随机变异是如何分布的

总体中单个变量的取值范围被称为正态分布，或钟形曲线。

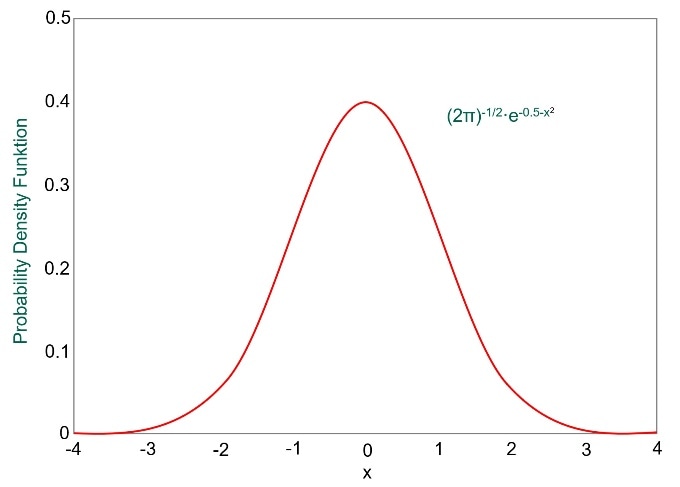
这的一个例子是高度。让我们说我们测量了所有女性的高度，然后绘制了在X轴上的高度的Y轴上的y轴的高度图。该图将具有上面的正态分布曲线的形状，显示了大多数具有平均高度的人在中心的平均高度以及非常高的女性的数量和非常短的女性尾随到任何一侧。

如果我们看一下正态分布曲线，我们可以看到形状越宽，远离均值的值就越多。而更窄的曲线意味着更多的值在均值附近。标准偏差，表示σ，给了我们一个数值，告诉我们如何展开的结果是。

对于正态分布，总是:

68.25％的结果将在平均值的标准偏差（1σ）范围内
95.45%的结果将在两个标准差(2 σ)范围内从平均值
99.73%的结果将在三个标准偏差(3 σ)从平均值

对于光谱学测量，标准偏差的值越小，正常分布曲线越窄，更精确的测量。标准偏差（σ）可以通过以下公式计算：

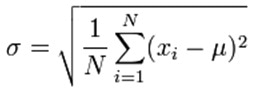
地点:

μ：人口意味着
x_我：个人测量值
N:测量次数

在现实世界中，我们通常不会测量整个群体。相反，我们测量的是总体样本。

在我们的光谱技术领域中，我们通常不会测量足够大的样本大小以准确计算整个人口的σ。相反，我们测量人口样本。幸运的是，我们可以使用略微修改的表达式来估计在这种情况下的样本标准偏差。我们使用符号年代表示样本的标准偏差。

s的表达是：

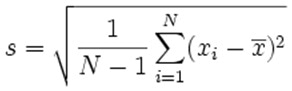
地点:

X̅:所有测量值的平均值
x_我：个人测量值
N:测量次数

我们可以使用此示例标准偏差来估计我们的错误余量光谱测量．如果我们想要95％肯定我们的结果 - 并记住，正常分布95.45％的结果将是与平均值的两个标准偏差 - 我们最终会得到：

浓度=<所有读数的平均值>% +/- 2 x s%

例如:要95%确定浓度是20% +/- 0.2,s必须等于0.1。

但是，对于光谱学这不够准确，并且我们需要考虑一个更多变量。这是我们将在下一个博客中涵盖的内容。

(CTA)

很快我们的指南“寻找真正的值”，我们涵盖基本统计数据，就绪。在此，我们通过实际光谱测量的示例工作，并解释当您没有所有信息时要做什么来估计您的测量结果的真实错误。如果你想得到下载副本，请在这里预先登记．

这些信息已被源，审查和调整了日立高科技分析科学提供的材料。欧洲杯足球竞彩欧洲杯线上买球

请使用以下格式之一在您的论文，纸张或报告中引用本文：

APA
日立高科技分析科学。欧洲杯线上买球（2020年1月15日）。光谱学统计概论。AZoM。从Https://www.wireless-io.com/article.aspx?articled=18479从//www.wireless-io.com/article检索。
MLA
日立高科技分析科学。欧洲杯线上买球《光谱学统计学概论》。氮杂．2021年7月04。< //www.wireless-io.com/article.aspx?ArticleID=18479 >。
芝加哥
日立高科技分析科学。欧洲杯线上买球《光谱学统计学概论》。AZoM。//www.wireless-io.com/article.aspx?ArticleID=18479。(访问2021年7月4日)。
哈佛
日立高科技分析科学，2020。欧洲杯线上买球统计光谱学概要．《AZoM》，2021年7月4日观看，//www.wireless-io.com/article.aspx?ArticleID=18479。