如今,几乎没有人会质疑,使用Mie理论提供了精确粒度分析的唯一途径,当使用激光衍射测量细颗粒。欧洲杯猜球平台激光衍射的国际标准规定,“对于小于50微米的粒子,Mie理论提供了最佳的一般解决方案”。欧洲杯猜球平台然而,这通常是一个很难满足的要求,因为Mie理论要求用户指定所研究材料的折射率(RI)。
如果用户正在测量无机化合物,则在标准文本如《儿童权利公约手册》或互联网上可以获得充足的数据。制药材料带来的问题更大,因为一欧洲杯足球竞彩种新的活性药物成分(API)的RI不太可能被知道。在这种情况下,诱惑是默认使用夫琅和费近似,虽然这是错误的,但被认为比“猜测”一个RI值更好。然而,这可能会导致在评估细颗粒组分时出现很大的错误,细颗粒组分是评估给定原料药的溶解度和生物利用度的关键参数。
用液体测量法测定折射率。
液体测量可以很容易和快速实现使用阿贝折射计,RI值的精度为小数点后4位。这远远超过了激光衍射所要求的精度,在那里,精确到小数点后2位通常被认为足以获得精确的结果。
粉末折射率测量
粉状材料的RI测定比较复杂。欧洲杯足球竞彩传统的方法依赖于单晶的形成或复杂的显微镜观察。在处理各种未知原料药的实验室中,这通常被视为一个不切实际的要求。然而,使用简单的折射计测量,可以在30分钟内计算出原料药的折射率。这里概述了这个过程。
Saveyn等人证明了水分散颗粒的体积RI可以通过测定颗粒在适当溶剂中溶解形成的溶液的RI来测定。已知溶质浓度记录的RI可以外推到100%浓度,以计算体积RI。
他们的工作包括在一系列不同溶剂中溶解的材料的例子。欧洲杯足球竞彩在每一种情况下,假定溶液表现理想,即没有强溶剂-溶质或溶质-溶质相互作用发生。这一假设通常适用于溶质浓度小于1wt%,其中RI随浓度线性变化。还确保被测材料不会被溶剂解离。
上面的假设对于api来说通常是有效的。大多数可溶于水,低浓度时RI随浓度呈线性变化。因此,Saveyn等人所描述的方法提供了一种快速、可靠的方法来确定精确粒度分析所需的RI值。下面给出了如何做到这一点的例子。
实验
采用Saveyn方法测定了两种通用原料药(赖诺普利和马来酸依那普利)的RIs。这些原料药的溶液是在0.1wt%到1wt%的去离子水中生成的。所得溶液的RI用阿贝折射仪测量,并外推至100%浓度,得到固体RI。
使用标准Becke Line显微镜测试对Saveyn方法获得的值进行验证。
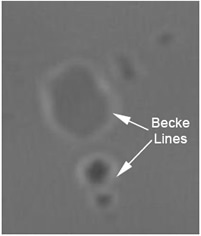
这依赖于观察靠近颗粒和悬浮液体界面的干涉带的位置(图1)。这个干涉带总是出现在RI最高的相中。对悬浮在不同RIs指数匹配油中的API颗粒进行了观察。欧洲杯猜球平台这使得可以确定干涉带从液体内部移动到粒子内部的液体RI。这提供了对粒子RI的精确独立测量。
|
图1所示。显微镜照片显示在液相中存在Becke线(liquid RI > Particle RI)。 |
结果赖诺普利
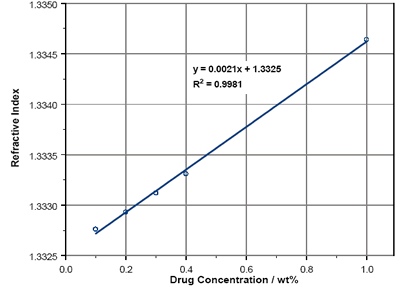
图2报告了赖诺普利溶液在0.1wt%到1wt%范围内的RIs。可以看出,在研究区域内,折射率与浓度呈线性相关关系。通过使用最佳拟合线方程(置信区间为99%),可以计算100%浓度下的RI。赖诺普利的RI为1.54。
|
图2.RIs赖诺普利解决方案。 |
上述预测的RI作为Becke Line研究的起点。贝克线的出现是在油的RIs范围从1.50到1.60。由此确定赖诺普利的实际RI在1.57 ~ 1.58之间。
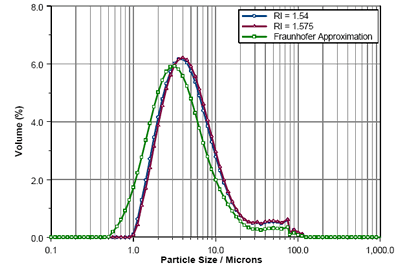
图3为激光衍射计算得到的粒径分布(Mastersizer 3000),使用Mie理论求得RI值为1.54和1.575。文中还给出了夫琅和费近似的结果。正如可以看到的,从折射计测量和贝克线研究预测的RIs产生了几乎相同的结果。然而,夫琅和费近似报告了更高的细颗粒分数,这可以从计算出的Dv10和Dv50值的偏移中得到证明(表1)。这表明了使用Mie理论的重要性。
|
图3.比较使用RIs为1.575,1.54和夫琅和费近似计算的赖诺普利粒径分布。 |
表1。赖诺普利的分布统计。
|
国际扶轮= 1.54 |
1.77 |
4.10 |
13.46 |
国际扶轮= 1.575 |
1.85 |
4.28 |
13.83 |
弗劳恩霍夫近似 |
1.26 |
3.17 |
10.11 |
马来酸依那普利结果
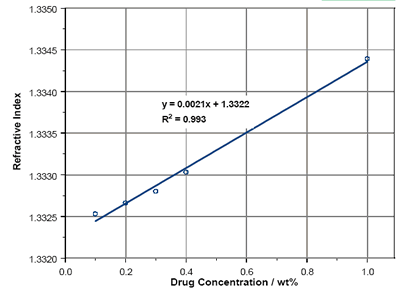
图4报道了马来酸依那普利溶液在0.1wt%到1wt%浓度范围内的RIs。与赖诺普利一样,在研究区域内RI与浓度呈线性关系。以100%浓度推算,RI为1.54。Becke Line测试提供的RI介于1.55和1.56之间。
|
图4.依那普利马来酸溶液RIs。 |
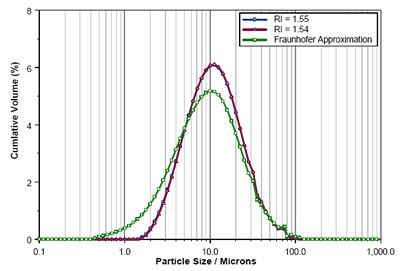
的Mastersizer 3000使用Mie理论得到的RI值为1.54和1.555的激光衍射结果,以及使用夫琅和费近似得到的结果如图5所示。同样,使用每个RI值得到的结果的差异是可以忽略的。然而,在使用Fraunhofer模型时,细颗粒被大量高估,导致报告的Dv10显著降低(表2)。
|
图5.使用RIs为1.55,1.54和夫琅和费近似计算的马来酸依那普利粒径分布的比较。 |
表2。马来酸依那普利的分布统计。
|
国际扶轮= 1.54 |
3.96 |
10.17 |
26.22 |
国际扶轮= 1.555 |
4.02 |
10.23 |
26.30 |
弗劳恩霍夫近似 |
2.56 |
8.73 |
25.68 |
结论
在使用激光衍射(Mastersizer 3000),如果要进行精确的细颗粒测量。然而,使用Mie理论时对RI值的精确要求常常迫使用户选择夫琅和费近似。
如图所示,简单的折射计测量提供了一种快速、可靠的方法来计算化合物(如药物活性物质)的RI,其精度足以用于激光衍射结果的计算。因此,没有必要依赖夫琅和费近似,允许用户避免与它的使用相关的错误。
.png)
这些信息已经从Malvern Panalytical提供的材料中获得,审查和改编。欧洲杯足球竞彩
有关此来源的更多信息,请访问莫尔文Panalytical.