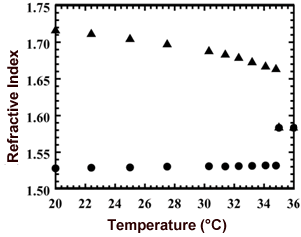
介绍光盘和衍射光栅是应用广泛的光学器件。目前光学器件的分析主要采用标量衍射理论和几何光学技术,因为折射型光学器件是根据折射理论设计的。最近,在精细结构建筑工程和计算能力方面的持续进步导致各种结构和设备的开发,这些结构和设备纤细和轻巧,拥有其他新功能。然而,认为有限差分时域(FDTD)方法[1,2]是因为衍射理论的弱性是波长尺寸结构的分析。时域有限差分法是一种在空间和时间上直接求解麦克斯韦方程组的有力方法。在该研究中,我们分析了激光诱导的液晶(LC)透镜[3,4]的光波传播,使用了二维FDTD方法。在染料掺杂的LCS(DDLC)中,在光热[5-8]中形成激光诱导的LC透镜。利用大的光学非线性和各向异性的复折射率,实现了激光诱导LC透镜的大范围变化。由于异常波的温度系数是负的,而普通波的温度系数是正的,所以这种特性与探测光束的偏振态密切相关。通过三维热传导分析[7,8]计算LC层中的温度分布。通过折射率的温度依赖性从温度确定折射率。通过FDTD方法分析折射率分布上的光波传播。此外,利用衍射理论计算了远场电场强度图[9,10]。 激光诱导的LC透镜向列相液晶(NLC)(4'-戊基- 4 -联苯碳亚硝酸盐,5CB)从默克日本公司获得。图1是测量到的5CB折射率的温度变化。根据制造商提供的物理特性数据,5CB的向列-各向同性转变温度为36℃。市上可得的分散红9 (DR9)从Aldrich公司获得,并用作掺杂染料,无需进一步纯化。DDLC夹在两个平行的透明玻璃基板之间。两种基板的内表面涂有薄的聚乙烯醇膜,单向摩擦,并且它们之间的空间由聚酯间隔物保持。在这种情况下,我们认为DDLC是一个单轴单晶,并定义了非凡的nE.和普通nO.根据强弱和弱吸收系数的折射率。染料浓度设定为0.8wt%20μm厚的样品。
|
图1。非凡的温度依赖性(▲)和普通(●)折射率的5CB。 |
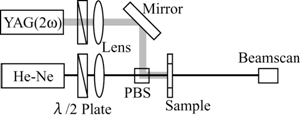
实验图2显示了由两个激光光源和DDLC单元组成的光学可控透镜系统。由于DDLC的电影很少氦-氖激光束(λ= 633nm)通过DDLC和滤光片,无吸收损耗。频率加倍的Nd: YAG激光束入射到与He-Ne激光束光斑相同的位置。频率倍增的Nd: YAG激光波长为532 nm, DDLC薄膜对532 nm波长的光强吸收。通过DDLC通过DDLC的频率加倍的Nd:YAG激光束被DDLC的过滤器完全切割。HE-NE激光束的功率为3.0 MW,而频率加倍的ND:YAG激光束的功率由可变ND滤光器变化。对倍频Nd:YAG激光束的偏振方向进行控制,使其与NLC定向器平行(= NLC的吸收轴)(非凡波),以有效地吸收激光束,而He-Ne激光束的吸收轴是非凡波。泵浦光强度在0 ~ 6 mW之间变化,初始焦距在3 cm左右。当探针He-Ne激光束的偏振方向平行于LC导向器时,在DDLC中形成一个凹透镜。通过扫描方法(Photon,Inc.:梁扫描模型1080),测量HE-NE激光束的光束直径作为观察点和DDLC样品之间的距离的函数。另外,由于频率加倍的Nd:YAG激光器引起的非线性相位调制,非线性相位调制,非凡波的焦点在DDLC的方向上移动。当探测器氦氖激光的偏振方向平行于液晶(异常波),主任的焦点异常波感动DDLC相反的方向,和焦点的光束直径增加随着功率的增加(图3)。当泵浦光束的功率超过几毫瓦时,焦点消失,探测光束扩散。这些效应与频率加倍的Nd:YAG激光器对DDLC薄膜中空间相位调制的影响有关。普通波的相位调制与特殊波的相位调制有很大的不同。在DDLC膜的非均匀照明(高斯型材)下,温度在照明区域中升高并最终调节,从而产生空间不同的折射率。
|
图2。激光诱导透镜在DDLC薄膜中的实验示意图。PBS:偏振分束器。 |

|
图3。非凡波(HE-NE激光)的直径与不同泵浦光束强度的传播距离(频率加倍:YAG激光)。 |
分析在这项研究中,我们使用了三维热传导分析来分析由光热效应引起的激光诱导的LC透镜中的折射率分布。三维热的结果时域有限差分(FDTD)方法采用电导分析。利用时域有限差分法分析了两片式透镜系统的光波传播特性。此外,我们使用衍射理论确定Z方向上的梁腰部的变化。 三维热传导分析是采用有限元法进行三维热传导分析,如图4所示。稳态三维热传导方程为: 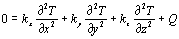 (1)
(1)
其中Q是介质中的热源,其从激光束提供。比例因子k一世(I = x, y, z)称为导热系数。为了解析求解图4所示几何形状的方程1,我们在以下边界条件下使用有限元法: 1.玻璃基板表面的温度等于室温。 2.-kLC(∂T信用证/∂n)B.= =GL.(∂t.GL./∂n)B.在DDLC和玻璃之间的接口。 3.(T信用证)B.= (TGL.)B.在DDLC和玻璃之间的接口。 由传播到DDLC膜中的激光吸收和高斯横向曲线产生的热源表示为:  (2)
(2)
在哪里ω是梁腰和我吗0.峰值强度。

|
图4。三维热传导几何分析。 |
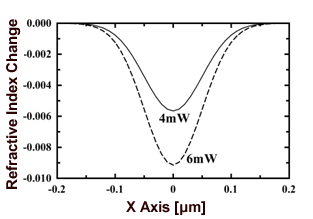
图5显示了不同泵浦光束强度的三维导热分析的结果。该折射率的折射率分布是X轴方向的分布[(y,z)=(0,6)]折射指数变化在样本中是最大的。由于泵浦光偏振异常,折射率变化呈负分布。当泵浦光束强度增大时,折射率变化变大,折射率峰值变小。计算得到的折射率分布用于射线矩阵计算和时域有限差分法。
|
图5。计算y=0和z=6时超常折射率随抽运光束强度x轴方向变化的空间分布[μM]。5CB / DR9膜的厚度为20μM,染料浓度为0.8wt%。 |
FDTD方法电场的入射光波是标准化的二维高斯梁: 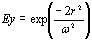 (3)
(3)
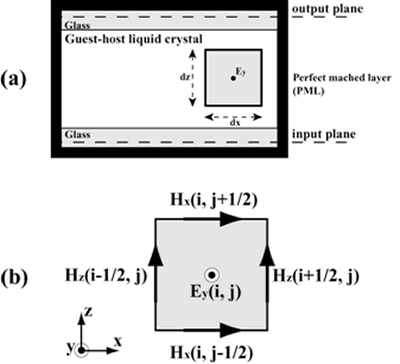
在哪里ω是根据1/e2电场强度。设定梁腰部,使强度分布成为115μm。我们在图6中显示了FDTD方法的分析区域。FDTD方法与eee算法一起使用。我们分析了TE波的测量结果。
|
图6。(a)FDTD方法中使用的计算空间的区域。(b)用于填补计算空间的YEE细胞。 |
光波传播由Maxwell等式控制:
由单轴各向异性大气LC的折射率分布,用公式5计算介电常数,并用于FDTD方法: 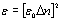 (7) (7)
由于测量系统是一个两片式透镜系统,我们设置了三个分析区域,每个区域有一个[空气-虚拟透镜-空气-玻璃]区域,一个[玻璃- LC -玻璃]区域,和一个[玻璃-空气]区域。每个假晶状体的焦距和束腰分别为3 cm和52μm分别。下一个区域的入射波是电流区域输出的电场分布。在这个分析中,我们假设每个区域没有边界反射。分析条件如表1所示。 表1。FDTD方法中使用的仿真参数。
|
细胞大小、Δx =Δz |
40海里 |
x轴的单元格数 |
6500. 260.μm |
z轴的单元格数 |
800 32.μm |
时间步,Δt |
0.9×10到16秒 |
PML板坯的厚度(细胞数) |
40 |
波长 |
632.8纳米 |
Beamwasit(HE-NE激光) |
115μm |
远场模式
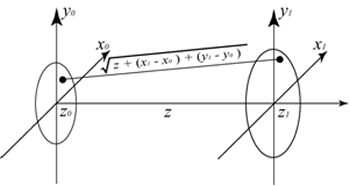
因为本研究的目的是分析光传播特性,所以我们计算了远场中的电场强度分布。但是,如已经众所周知的,FDTD方法需要很大的计算机硬件容量。因为在这种尺寸的空间中执行计算是不可能的,我们使用衍射理论来确定远场的电场强度分布。数据处理程序如下: 1.结果是在z=z的平面上用FDTD方法得到的0.。注意,这个值是真实的。 2.快速傅里叶变换(FFT) Ey (x0.,t)在时域中完成,其第一阶系数被认为是转换ey(x0., t)进入复振幅: 3. ẽy(xO.) = FFTT.[Ey(xO.,t)](8) 在哪里ẽy(xO.)是复杂价值。 4.振幅和角度在观测平面上,通过时域FFT得到电场的分布。利用夫琅和费衍射计算得到远场图。衍射几何形状如图7所示。 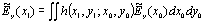 (9)
(9)
地点:

|
(10)
|
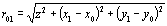
|
(11) |
5.强度分布在z=z1获得: 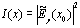 (12)
(12)
|
图7。衍射几何形状。 |
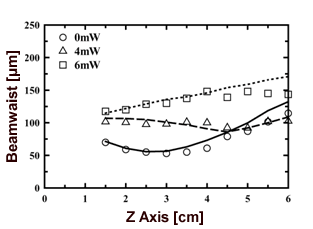
结果与讨论图8显示了采用时域有限差分法和测量结果进行分析后梁腰的变化。符号是测量结果,泵浦光强度分别为0、4和6mW。一条线是时域有限差分法和衍射计算的分析结果。为了分析每个泵浦光束强度的测量结果,确定了在DDLC中的折射率变化。因此,当形成如图9所示的折射率分布时,分析结果是满意的。然而,这种折射率分布与通过导热分析获得的折射率分布不同。
|
图8。光束束腰和焦点(z轴)对泵浦光功率的影响。符号和线分别表示实验和衍射理论FDTD方法的结果。 |
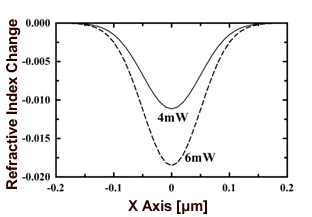
|
图9。时域有限差分法得到的折射率变化。 |
折射率差异为10-3。室温下液晶的折射率变化主要是由光束束腰和泵浦光的强度引起的,在温度变化范围内液晶的折射率也会发生变化。然而,我们认为这种折射率变化的影响很小,因为梁腰部,泵浦光束强度和室温是测量条件。因此,我们研究了LC折射率的温度变化,并考虑了使用FDTD方法获得的折射率分布的性质。使用楔形方法结果将FDTD方法结果进行比较的方法。我们通过楔形法测量了我们在导热分析中使用的折射率的温度变化。计算折射率的温度变化:
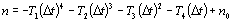
|
(13)
|
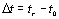
|
(14) |
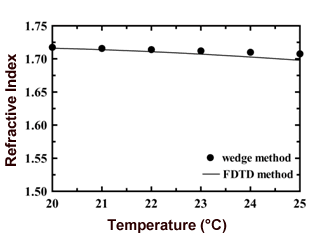
其中T一世(i=1,2,3,4)是温度系数tR.是半径的温度,而n0.和t0.分别为折射率和折射率分布中心的温度。图10显示了液晶折射率的温度变化。如图10所示,由于折射率的两种温度变化之间没有差异,我们认为FDTD方法提供的折射率分布结果是正确的。
|
图10。向列液晶折射率的温度变化。(●)楔形方法(-)FDTD方法。 |
结论在本文中,我们研究了FDTD方法对液晶装置的有效性。分析了非线性光学效应中最基本的光热效应所形成的激光诱导LC透镜的光传输特性。通过三维导热分析,计算通过LC层中的泵浦梁形成的温度分布,并获得折射率分布。利用折射率分布分析了光在液晶层中的传播特性。此外,我们对电场振幅分布的FDTD分析结果进行了快速傅里叶变换,以计算束腰在远场。利用衍射理论计算了场强分布。 最后给出了测量结果,验证了时域有限差分法的有效性。 参考文献1.Morisaki和H. Ono,“主-主液晶中产生的激光诱导透镜的分析”,电子与信息科学学报,vol . 32, no . 1, no . 2。 2.Morisaki和H. Ono,“偏振对光在激光诱导晶体中传播的影响”,J.应用。理论物理。, 95(2004) 3279-3284。 3.沈玉仁,“离焦液体介质中激光诱导衍射图形的形成”,光子学报。, 6(1981) 411-413。 4.刘天华,严佩英,R. R. Michael和G. M. Finn,“横向自相位调制和非线性薄膜传输中的双稳性”,J. Opt. Soc。点。, b4,(1987) 886-891。 5.“热传导分析在主-主液晶中的光热效应特性”,J. Opt. Soc。点。, b 16(1999) 2195。 6。H. ONO和K.Shibata,“通过光热自衍射技术同时测定液晶的各向异性热导体”J. phy。d,appl。物理。,33(2000)137-140。 7。T. Uno,“电磁场时域有限差分法”,CORONA出版公司,(1998) 8。Emmanouil E. Kriezis和Steve J. Elston,“通过二维时域有限差分方法在液晶显示器中的光波传播”,Opt. Commun。, 177(2000) 69-77。 9。Ichikawa和Y. Sugimoto,“用于CWDM器件的毫米尺寸微菲涅耳透镜的电磁数值表征”,Opt. Commun。, 234 (2004) 10. Terman,F. E.,傅里叶光学介绍(McGraw-Hill),1968年。 联系方式 |