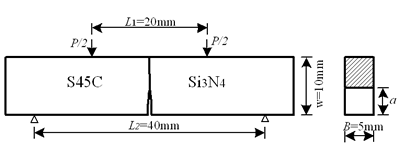
我ntroduction由于陶瓷在高温下具有稳定的机械性能,并且对磨损,侵蚀和氧化具有良好的耐药性,因此陶瓷/金属接头越来越多地应用于广泛的工程领域。However, the difference of material properties between metal and ceramic induces stress singularities at the interface edge.此外,由于热膨胀系数不匹配,在冷却过程中将诱导高热残留应力。这stress singularity together with the thermal residual stress degrades the strength of ceramic/metal joint and makes the evaluation of the strength difficult.关于残余应力和陶瓷/金属关节的强度评估,已经完成了许多工作。例如,Kobayashi等人。[1,2]研究了Si的弯曲强度和残余应力3n4/s45c关节和样品大小对弯曲强度的影响。Qiu等。[3]研究了残留应力和循环负荷对Si强度的影响3n4/S45C joint.但是,由于问题的复杂性,尚未提出针对陶瓷/金属关节的广义评估方法。 这elastic solution of the singular stress field of the interface crack has been studied since 1959 [4-9].赖斯[10]总结了该领域的工作,并为界面裂纹设置了弹性断裂力学概念。Yuuki等。[11,12]提出了基于弹性理论预测陶瓷/金属关节强度的最大正常应力标准。这plastic deformation of metal will inevitably appear near the crack tip due to the stress singularity.For most of the ceramic/metal joints, the plastic deformation of metal has a significant influence on the strength of the ceramic/metal joint.由于分析复杂性,尚未根据弹性理论评估陶瓷/金属关节的断裂路径和强度。 我n this study, four point bending tests of Si3n4/S45C joint specimens with an interface crack were carried out.evaluation of the fracture path and fracture toughness was attempted based on the elasto-plastic analysis. 实验标本准备图1显示了Si的几何形状和尺寸3n4/S45C joint specimen.用银基合金(WT%为:Ag,71%,Cu,27%,Ti,2%),厚度为60μm3n4ceramics and S45C steel.悬挂在真空炉中(2.5x10-5Torr).炉子的温度以20速度升高oc/min到850的老板温度oC并保持10分钟,然后以10速度降低oc/min。连接表面用直径为0.25μm的钻石粉抛光。在悬挂期间,施加了0.002 MPa的接触压力。 悬挂后,通过电气排放方法引入了界面裂纹,切割线直径为0.1 mm。制备了四个具有不同裂纹长度的标本。两个样品的裂纹长度为4.0 mm,其他两个样品的裂纹长度为1.0 mm和2.0毫米。
|
图1。断裂韧性标本。 |
实验结果Four point bending tests were carried out on the fracture toughness specimens at a crosshead speed of 0.5 mm/min.Table 1 shows the results of the fracture toughness.明显的断裂韧性定义为: 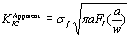 (1) (1)
with 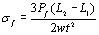 (2) (2)
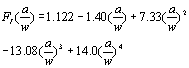 (3) (3)
where PF是断裂载荷,A是裂纹长度,标本宽度,t标本亮度,l2外部跨度和L1the inner span. Table 1.裂缝韧性测试的结果。
|
1 |
1。0 |
285.4 |
17。128 |
1。0436 |
0。9807 |
2 |
2。0 |
237.8 |
14.27 |
1.0530 |
1.1607 |
3 |
4。0 |
1649.0 |
98.95 |
1。2561 |
12.4317 |
4 |
4。0 |
1744.2 |
104.65 |
1。2561 |
13。1478 |
As can be seen in Table 1, the specimens with a crack length of 4.0 mm indicate a higher fracture load than those with shorter crack lengths of 1.0 and 2.0 mm.As the residual stress will redistribute after cutting [2], the relaxation of thermal residual stress for longer crack length may be a possible reason. 图2显示了骨折标本的宏观观察。For the specimens with a crack length of 1.0 and 2.0 mm, crack propagated into Si3n4directly from the initial crack tip in the direction of about 40o。For the specimens with a crack length of 4.0 mm, the crack propagated along the interface for about 1.0 mm and then kinked into Si3n4在大约10个方向上o到界面。

(a)a = 1.0mm 
((b) a = 2.0mm 
((c) a = 4.0mm 
(d)a = 4.0mm |
图2。骨折标本。 |
Oscillatory Singular Stress Field of The Interface Crack and The Maximum Normal Stress Criteria这elastic solution of the stress field of an interface crack has been accomplished by the Willims [4], Erdogan [5, 6], England [7] and Sih et al. [8, 9].我t has been found that the stress field near the interface crack tip has the oscillatory singularity.Under the polar coordinate with the origin located at the crack tip, the stress field can be expressed as 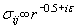 (4) (4)
这里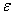 是可以表达为的双材料常数
是可以表达为的双材料常数 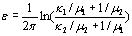 (5) (5)
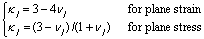 ((6) ((6)
在哪里µjandvj剪切模量和泊松的比例分别为材料。欧洲杯足球竞彩 振荡性奇异应力场的应力强度因子定义为 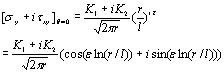 ((7) ((7)
在哪里,l是消除振荡期限的参考长度。通常l占整个裂纹长度的值,即l = 2a。 当知道界面的应力时,可以将应力强度因子推断为: 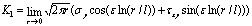 ((8) ((8)
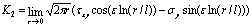 ((9) ((9)
Yuuki等。[11,12]提出了界面裂缝断裂的最大正常应力标准。考虑到价值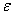 很小,正常应力大约表示为
很小,正常应力大约表示为 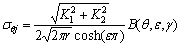 ((10) ((10)
在哪里 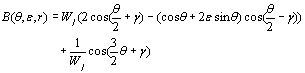 ((11)
((11)
w1= e-ε(π-θ), W2= eε(π+θ)((12) 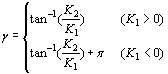 ((13) ((13)
这direction of the maximum normal stress can be determined from: ∂b(θ,ε,y)/∂θ= 0((14) 令θ0represent the direction of the maximum normal stress, the corresponding stress intensity factor can be expressed as: 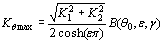 ((15) ((15)
裂缝将沿着θ0当kθmax到达K。我C基本材料的价值。应该注意的是,当θ0变得小于某些值,因为界面的强度通常低于基本材料的强度。 界面裂纹尖端处的弹性塑料奇异应力场已发现线性硬化材料的弹性塑料奇异应力场[13]基本上与弹性材料的弹性材料的定义为:  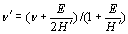 ((16) ((16)
在哪里e一世s the Young’s modulus and H’ the hardening coefficient. 这refore, the elasto-plastic singular stress field at the interface crack tip is substantially the same as the elastic singular stress field of the interface crack tip.这governing region of the elasto-plastic singular stress field will be confined in a small region around the crack tip inside the yield zone.对于陶瓷/金属关节,考虑到硬化系数的值远低于Young模量的值,因此可以从等式中找到。(16)和等式。(5) 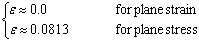 ((17) ((17)
FeM Analy基于弹性塑性应力强度因子的SIS和骨折路径和韧性的评估FeM analysis was carried out under plane stress condition using the program of ABAQUS.si3n4一世s assumed as an elastic material whose material constants are independent of temperature and E=289 GPa,v= 0.25,CTE = 4.2x10-6。S45C steel is assumed as a linear hardening material with the material constants listed in Table 2 [14].自由温度被认为是550oC用于分析热残留应力。 Table 2.S45C的材料常数
|
e((GPa) |
206 |
206 |
201 |
197 |
192 |
187 |
183 |
v |
0。3 |
0。3 |
0。3 |
0。3 |
0。3 |
0。3 |
0。3 |
σy-(MPA) |
375 |
348 |
333 |
309 |
280 |
241 |
193 |
H’(MPA) |
1381 |
2056 |
2680 |
2325 |
1685年 |
1026 |
687 |
CTE(10-6) |
11.71 |
12.17 |
12.63 |
13.09 |
13.55 |
14.01 |
14。47 |
为了进行比较,还进行了弹性分析。根据25的弹性常数计算oC,双材料常数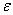 对于弹性情况为0.01588。表3列出了应力强度因子以及通过弹性分析获得的最大正常应力的方向。可以发现
对于弹性情况为0.01588。表3列出了应力强度因子以及通过弹性分析获得的最大正常应力的方向。可以发现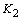 value due to residual stress is much higher than
value due to residual stress is much higher than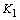 and the values of θ0由于残留应力几乎相同,约为70o。裂纹长度为2.0毫米的样品具有K的最大值θmax由于残留应力。k的值θmax由于残留应力和裂缝韧性测试期间的施加应力叠加,由于残留应力而接近。
and the values of θ0由于残留应力几乎相同,约为70o。裂纹长度为2.0毫米的样品具有K的最大值θmax由于残留应力。k的值θmax由于残留应力和裂缝韧性测试期间的施加应力叠加,由于残留应力而接近。 表3。Stress intensity factors and the direction of the maximum normal stress according to the elastic analysis.
|
a=1mm |
k1= 1.50 k2= 21.05 |
25.79 |
69o |
k1= 2.5 k2=21.7 |
26.45 |
68o |
a = 2mm |
k1= 0.5 k2= 25.4 |
29。52 |
70o |
k1= 1.63 k2= 25.42 |
30。21 |
69o |
a=4mm |
k1= -0.01 k2=24.8 |
28。54 |
71o |
k1= 14.0 k2= 25.1 |
37.69 |
61o |
但是,弹性分析的结果显然与K的值相矛盾θmax远高于k我Cvalue of Si3n4,大约6.0 mpa√M [15]。Also, the elastic analysis cannot explain why the specimen with a=4.0 mm indicates higher fracture load than the specimen with a=1.0 mm since Kθmax由于A = 4.0 mm的残余应力大于A = 1.0 mm的应力。 F一世gures 3 and 4 show the stress distribution the interface obtained by the elasto-plastic analysis.在图中还绘制了带有–0.5斜率的线。we can see that the curves are almost parallel to the reference line in the region r<10-6m, which indicates that the stress near the crack tip is dominated by the elasto-plastic singular stress field.

|
图3。沿界面的正常应力分布。 |

|
F一世gure 4.沿界面剪切应力分布。 |
图5和6显示了由等式定义的未耦合组件。(8)和等式。(9)。Different from the elastic case, here the reference lengthltakes thevalue of 1.0-6M,接近弹性塑料奇异应力场的管理区域的大小。图5显示了由于残留应力引起的应力分布,图6显示了由于残留应力和施加载荷而引起的应力分布。可以发现曲线几乎平行于区域r <1.0中的参考线-5m.


|
F一世gure 5.沿界面沿界面分布的分布,以使残余应力分布。 |

|
F一世gure 6.在试样断裂处沿界面沿界面分布的分布。 |
表4列出了通过弹性塑料分析获得的应力强度因子和最大正常应力的方向。我t can be found thatkθmax由于残留应力降低,a = 2.0 mm的序列,a = 1.0 mm和a = 4.0 mm。This result can explain why the specimen with a crack length of 4.0 mm indicates higher fracture load compared to the other specimens.这applied load tends to decrease the value of K2。k的减少2对于A = 4.0 mm特别明显,θ值0For a=4.0 mm is 33o, which is much smaller than those for a=1.0 mm and a=2.0 mm.This agrees with the experimental result, where the specimens with a=1.0 mm and a=2.0 mm fractured with an angle of about 40o从界面中,当a = 4.0 mm的样品沿界面断裂。值kθmax由于残留应力和施加应力,即裂缝发生时,无论裂纹长度如何,几乎都是相同的。这y are also close to the K我Cvalue of Si3n4,虽然少于它。Kobayashi等[1]在Si的弯曲测试中发现3n4/s45c关节可以将结果分为两组,其中一组显示出相对较高的强度,另一组显示出非常低的值。低强度的原因之一被认为是陶瓷中存在裂纹的原因,因为在连接后切割过程中很容易从固有的缺陷中引发裂缝。This can be also considered to be one of the reasons why thekθmaxvalues when fracture occurred are less than the K我Cvalue of Si3n4。 Table 4.根据弹性塑料分析,应力强度因子和最大正常应力的方向。
|
a=1mm |
k1= -0.15 k2= 2.51 |
2。68 |
71o |
k1=0.43 k2= 2.50 |
3。09 |
67o |
a = 2mm |
k1= -0.22 k2= 2.80 |
2。95 |
71o |
k1= 0.78 k2= 2.76 |
3。65 |
65o |
a=4mm |
k1= -0.30 k2= 2.45 |
2。51 |
72o |
k1= 3.82 k2= 0.76 |
4.28 |
33o |
结论在SI上进行了断裂韧性测试3n4/S45C joint specimens with interface cracks of different lengths. Evaluation of fracture path and fracture toughness was carried out based on elasto-plastic analysis in which S45C steel was assumed as a linear hardening material.获得的结论可以总结为: •热残留应力对关节的断裂韧性具有显着影响。Due to the effect of residual stress, the specimen with a crack length of 4.0 mm has higher fracture toughness than those with crack lengths of 1.0 mm and 2.0 mm.裂纹传播到Si3n4直接从40个方向的初始裂纹尖端oFor crack lengths of 1.0 mm or 2.0 mm, while it propagated along the interface for the crack length of 4.0 mm. •裂纹尖端附近的应力由弹性塑料奇异应力场主导。最大限度σθ基于弹性塑料奇异应力场的标准可以成功地用于评估断裂路径和断裂韧性值。3。kθmax由于残留应力而导致的值降低了A = 2.0 mm,A = 1.0 mm和A = 4.0 mm的序列。This is the same sequence of fracture load of the specimens with a=2.0 mm, a=1.0 mm and a=4.0 mm.施加的应力导致K值的下降2。k的减少2For a=4.0 mm was significant and the value of θ0对于A = 4.0毫米,对于A = 1.0毫米和A = 2.0毫米的= 4.0毫米。This agrees with the experimental result that the specimens with a=1.0 mm and a=2.0 mm fractured with an angle of about 40oto the interface, while the specimens of a=4.0 mm fractured along the interface.这kθmaxvalues at the fracture of specimens were almost same for all the specimen and were close to the K我Cvalue of Si3n4。 参考1。H. Kobayashi, Y. Arai, H. Nakamura and T. Sato, “Strength Evaluation of Ceramic-Metal Joints”, Materials Science and Engineering, A143 (1991) 91-102. 2。H. Kobayashi,H.,Nakamura,A。Todoroki,W。Park,T。Koide和H. Taniai,截断标本的影响和大小对陶瓷/金属关节的弯曲强度,Trans。JSME,A60-569(1994)65-70。 3。J.H.Qiu,S。Nakamura,M。Kawagoe和M. M. M. M. M.,“连接Si3n4/S45C强度对残留应力的影响”,《无机材料杂志》,13-4(1998)167-172。欧洲杯足球竞彩 4。M.L. Williams, “The Stress Around a Fault or Crack in Dissimilar Media”, Bulletin of the Seismological Society of America, 49-2 (1959) 199-204. 5。F。erdogan, “Stress Distribution in Bonded Dissimilar Materials with Cracks”, J. Appl. Mech., 32 (1965) 403-411. 6。F。erdogan, “Stress Distribution in Bonded Dissimilar Materials Containing Circular Ring-shaped Cavities”, J.Appl.Mech., 32 (1965) 829-836. 7。A. H. England,“不同媒体之间的裂缝”,J。Appl。Mech。,32(1965)400-407。 8。GC。Sih和J. R. Rice,“带有裂纹的不同材料板的弯曲”,J。Appl。欧洲杯足球竞彩Mech。,31(1964)477-483。 9。J. R. Rice and G.C.SIH,“不同介质中裂纹的平面问题”,J。Appl。Mech。,32(1965)418-423。 10。J. R. Rice, “Elastic Fracture Mechanics Concepts for Interfacial Cracks”, J. Appl. Mech., 55 (1988) 98-103. 11。R. Yuuki和J.Q.XU,英格。分数。Mech。,“界面裂纹基于应力的标准在不同材料中的界面中串联出来”,41-5(1992)635-644。欧洲杯足球竞彩 12。R. Yuuki,J.Q。Xu和Y. Mutoh,“基于界面断裂力学的金属/陶瓷键关节的断裂和强度的评估”,Trans。JSME,A60-569(1994)37-45。 13。J.Q.Xu和L. Fu,“”Stress Field near an Interface Edge of Linear Hardening Materials”,,智格大学杂志:科学诉3-1(2002)13-18。欧洲杯线上买球 14。N. Okabe,M。Takahashi,X。Zhu,K。Kagawa和M. Maruyama,“陶瓷/金属关节的残留应力和疲劳强度特性”,J。Soc。垫。科学,日本,48-12(1999)1416-1422。 15。y。Mutoh and I. Yumoto, “Fracture Toughness Evaluation for Ceramics/Metal Joints”, Trans. of the Symposium of Material Mechanics of JSME, No.900-50 (1990) 185-190. 联系方式 |