介绍为了延长电池寿命的便携式电动工具,节省电力消耗的设备是一个非常重要的话题,即使对于液晶显示器(LCD)。液晶是用于各种用途,特别是对于移动应用程序,因为它的重量轻和低耗电量。现在,双稳态液晶显示器类型,如一个方位的双稳态显示器(ZBD)[1]引起了极大关注。ZBD设备基于地表起伏光栅对准展示了良好的图像质量和记忆能力。然而,对齐的确切机制仍然是一个有争议的话题。哈勒姆和Sambles安排争论关于拓扑一致性模型[2]。方位锚定在他们的文章中,表面能量的函数计算光栅高度Berreman的拓扑一致性模型的基础上液晶(LC)弹性理论[3]。从计算和实验结果的对比通过光学制导模式技术,一个好的协议为浅振幅光栅被发现,而不是更大的振幅光栅。他们列举这种差异的可能原因,和更全面的需求拓扑描述模型。矛盾的一个可能的原因可能是由于实验准确性较低。另一个验证实验是必需的。 有限元法(FEM)被广泛用于解决两个——和/或三维问题。液晶对齐也可以通过有限元仿真分析。最近,一个表面的饱和趋势方位锚定能量作为光栅的高度的函数很好证明了数值模拟有限元[4]的基础上。此外,一个好的协议与有限元计算和实验结果也显示不仅对浅振幅光栅表面,而且对深沟光栅。 本文依赖的形状表面光栅表面方位锚定能量有限元研究,考虑到实际光栅表面。 有限元方法分析二维正弦救援光栅表面上导演安排,二维有限元法(FEM)使用基于弹性理论和能量最小化原理。图1展示了一个典型的二维有限元模拟结果,在网30x 10节点安排。棒在图1代表董事LC, LC分子的中心对应的节点。一个周期边界条件应用到左边,对吗t侧侧边界。关于上边界条件,LC董事将平行排列在玻璃衬底,对应于导演安排的。 
图1。典型的二维有限元模拟结果。杆代表了LC导演。 关于降低边界面,一个正弦救援光栅被认为与音高的正弦光栅,P对应于网格的一个周期。在底面上的所有节点,如图1所示,平行排列的LC分子固定边界条件假设。因为,分子排列垂直于山脊线,弹性变形能量最大。在考虑区域e,当θ(x, y)作为一个函数的位置(x,y)是由导演和之间的角度定义的x轴,弗兰克的弹性能量密度可以派生[5], 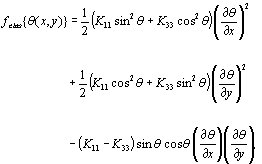 (1)
(1)
K11和K33斜面和弯曲变形的弹性常数[5]。有限元法的矩阵可以线性近似的可控性θ(x, y)。是过去文献[3]中描述,如果分子说谎脊平行,没有畸变能在地表附近。f濒危语言联盟代表了额外的弹性能量par单位面积,可以使重定向发布的分子沿着山脊平行。即。,the濒危语言联盟tic distortion energy in the considered area e corresponds to the surface azimuthal anchoring能量函数8。当F8表达的是 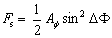 (2)
(2)
在哪里ΔΦ是导演和山脊线之间的偏差角,表面方位锚定能量系数φ可以获得的  (3)
(3)
自ΔΦ= 90˚条件下在我们的研究[2,3]。因为,如公式(2)所示,估计F年代是最大的ΔΦ= 90˚。 与Berreman的模型的结果比较,计算方位能量锚定也由以下方程[3];  (4)
(4)
在哪里h光栅的高度,Λ光栅的间距和K = (K11+ K33)/ 2。LC材料的弹性常数欧洲杯足球竞彩K11和K33被小山的初步测量方法和表1中列出。 表1。LC材料的弹性常数欧洲杯足球竞彩
|
多层陶瓷- 2051 |
10.4×10-12年N |
15.6×10-12年N |
5 cb |
7.12×10-12年N |
9.82×10-12年N |
实际救援光栅的形状形成的实验是不对称的,而不是正弦。调查的依赖的形状表面光栅表面方位锚定能量,不对称正弦光栅和梯形形状的光栅表面,如图2和图3所示,参数W和D代表的比例不对称P。 
图2。不对称的正弦光栅的形状计算在这个研究。 
图3。梯形的形状光栅计算在这个研究。 实验光栅用于我们的实验被光刻胶组合(·希普利S1830)。在涂布光刻胶电影在硼硅酸盐玻璃衬底,全息紫外线辐照光致抗蚀剂膜。 图4显示了全息光的实验装置。 
图4。实验装置的全息紫外线 光栅是利用两个线性偏振,相互连贯的cw氦镉激光(Kimmon K3501R-G),其波长λ= 325海里。Λ是由交叉角吗θr两个激光束之间,所描述的 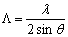 (5)
(5)
当我们进行这些实验Λ= 2,3,4μm分别。光栅的高度是由紫外激光束的强度控制。完成紫外线照射后,光栅的平均身高是由原子力显微镜测量(日本岛津公司spm - 9500 J2)。 扭曲向列液晶样品细胞制造结合光栅衬底,另一个玻璃衬底的聚乙烯醇(PVA)涂层和pre-rubbed。名义上的细胞间隙是25μm。化学特性可能锚定能源起着重要的作用。尤其是表面润湿性能的影响和表面吸附的锚定能量已经争论了十年。因此,两种向列LCs,混合物(多层陶瓷- 2051,默克公司日本)和4-cyano-4 -n-pentylbiphenyl (5 cb,默克公司日本),被雇佣。前者是散装过渡类型(相对低润湿性)LC,后者是表面过渡类型(高向列润湿性)LC [7]。 方位能量测量锚定转矩平衡方法[8]。偏差角ΔΦ山脊的光栅表示方位能量锚定一个φ由救援光栅引起的。在这里,我们假设方位锚定在PVA对光栅表面表面相对强劲。[9]一个φ是由之间的平衡扭矩由于散货,由于表面锚定。方位锚定能φ可以从向列液晶的弹性理论[8]  (6)
(6)
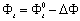 (7)
(7)
在哪里d是细胞厚度,Φt实际的扭曲和什么Φt0是按摩治疗的方向之间的夹角PVA对齐,电影和山脊线的光栅。在我们的实验中,与前面的文章[8],钨灯作为一种白色光源是为了避免使用错误的强吸收的光致抗蚀剂的影响。由于测量细胞很厚,它满足Mauguin[10]的条件,Φt对应于发现灭绝之间的角位置旋转偏振器和分析器。 结果与讨论图5显示了数值结果表面的方位锚定能量的函数计算的光栅高度Berreman的模型和有限元法。光栅的间距应该是2、3和4μm。LC材料多层陶瓷- 2051。从图5中,饱和趋势面方位锚定能量作为光栅高度的函数被发现在这两种计算方法。虽然计算有限元饱和趋势显著大于Berreman计算的模型,似乎是相互一致的两种计算方法。实验结果也标注在图5。从我们的实验结果,0.2的高度~1.5μ在计算m光栅显示良好的协议。 
图5。实验和数值结果表面方位能量锚定Berreman光栅高度的函数计算的模型和有限元法,LC材料多层陶瓷- 2051。 来验证我们的考虑,使用5 cb进行了另一项研究。强调不同的饱和趋势,不同于Berremen最初的线性依赖关系,结果光栅高度和的平方φ如ref。[2]如图6所示。不管LC材料,大幅度的饱和趋势光栅表面和一欧洲杯足球竞彩个好的协议之间的数值和实验结果浅光栅表面显然是公认的。这个结果表明,弹性能量占主导地位,而不是化学性质,除了意想不到的表面条件如强homeotropic对齐在光栅表面。 
图6。实验和数值结果表面方位锚定能量平方的函数Berreman光栅高度计算的模型和有限元法,其中LC材料5 cb。 不对称正弦光栅可以很容易地得到的全息浮雕光栅照射角度将不对称。图7显示了数值结果表面的方位锚定能量造成的不对称正弦光栅光栅高度的函数计算的有限元法,对LC材料为多层陶瓷- 2051。发现不对称正弦光栅显示强大的方位能量锚定。 
图7。数值结果表面方位锚定能量造成的不对称正弦光栅光栅高度的函数由有限元计算。 经常看到通过使用电子显微镜,光刻胶是梯形的形状而不是矩形。因此,救援光栅的形状由光掩模过程似乎是梯形。图8显示了数值结果表面的方位锚定能量造成的梯形光栅光栅高度的函数的有限元计算。当光栅的形状是三角形(D = 0),方位锚定能量相对较小,而且取决于光栅的高度。另一方面,当光栅的形状是长方形(D = 0.5),方位能量锚定强,减少对光栅的高度敏感。这是因为我们认为导演略高于表面往往谎言沿着表面平行,因此,董事附近的侧表面矩形将正常的底物。导演简介由有限元计算如图9所示,D = 0.4。发现导演概要文件由有限元计算是公正的和适当的。 
图8。数值结果造成的表面能量方位锚定梯形光栅光栅高度的函数由有限元计算。 
图9。董事资料计算的有限元法(D = 0.4)。 结论正是验证了有限元Berreman拓扑一致性模型适用于浅光栅表面。理论分析和实验结果之间的分歧由裁判。[2]似乎Berreman限制的模型,而不是造成实验失败。简单近似表面锚定公式Berreman一样相似水平的评价可以解释这样的饱和趋势,锚定效应是由弹性而不是化学性质。设计方位表面锚定能任意表面浮雕光栅的形状,有限元法可以是一个强大的工具。跟踪后,因为真正的表面通过使用原子力显微镜,追踪模式可以直接输入到有限元法和表面方位锚定能量可以通过有限元预测。 确认我们感谢h . Ichinose先生(默克公司日本)提供LC材料。欧洲杯足球竞彩这项工作是支持的补助金(No.15760020)日本年轻科学家(B)促进社会科学。欧洲杯线上买球 引用1。g . p . Bryan-Brown c . v .布朗,j·c·琼斯,e . L。木头,i c .鼠尾草,Brett和j·p·鲁丁,“光栅双稳态向列对齐装置”,社会信息显示的97年消化,(1997)p.37-40。 2。b·t·哈勒姆和j·r·Sambles“槽深度依赖锚定强度的零阶grating-aligned”液晶,液晶,27(2000)1207 - 1211。 3所示。D.W. Berreman”,固体表面形状和相邻的向列液晶的排列”,理论物理。(1,28(1972)1683 - 1686。 4所示。y太:田中,m .木村和t . Akahane“表面方位光栅表面之间的锚定能源和向列液晶层有限元方法研究”,日本。j:。理论物理,43(2004)4310 - 4311。 5。f·c·弗兰克,“液晶:液晶理论”,阀瓣。法拉第Soc。,25(1958) 19-28. 6。K .小山m . Kawaida和t . Akahane”方法测定弹性常数K1K2K3向列液晶的使用均匀一致的细胞”,日本。j:。理论物理,28(1989)1412 - 1416。 7所示。美国奥卡河,t . Mitsumoto m .木村和t . Akahane”之间的关系年代urfaceo请和年代urface一个zimuthal一个nchoring年代实力的nematicliquidcrystals》。启E,69年061711 (2004)。 8。t . Akahane金子h . m .木村,“小说的方法测量表面扭转向列液晶的锚定强度”,日本。j:。理论物理,35(1996)4434 - 4437。 9。k大m .木村和t . Akahane”,真正的方位测量锚定能量考虑液晶分子吸附在对齐电影”,日本。j:。理论物理,42(2003)6428 - 6433。 10。c·h·古奇和H.A.逗留o立足properties的t知道nematicliquidcrystal年代tructures与t知道一个角≤90年°”,期刊。D8(1975)1575 - 1584。 详细联系方式 |