介绍超声波在材料科学中的应用越来越多欧洲杯线上买球唱歌。利用超声波在有机合成、聚合物反应、电镀、电合成、电聚合等方面的作用，取得了较好的效果。研究表明，超声辐照可用于聚合物的降解。化学键的破损是由于空化入培养基。空化是小气泡的形成和剧烈崩溃。这导致足够大小的剪切力，以引起化学键的破裂[2]。Price[2]对超声降解聚合物的研究进行了综述。研究了各种参数，如温度，超声强度，溶液蒸气压，超声波和聚合物浓度的频率[2，3]。 然而，到目前为止，已经看到了没有关于（氯化聚丙烯）CPP的超声降解的报告。氯化聚丙烯具有优异的耐磨性，年龄抗性和酸和碱性耐药性。它还具有优异的聚烯烃粘附性。作为粘合促进剂，CPP广泛用于聚烯烃涂料，凝集剂，印刷油墨和相容助剂等。近年来，人们对CPP的研究进一步了解聚烯烃的快速发展[4]。为了拓展CPP的研究领域，本文介绍了超声降解CPP在甲苯溶液中的研究。为了确定动力学方程是超声劣化研究的重要基础工作。本工作的目的是准确地确定超声辐照下甲苯溶液中CPP的动力学方程。 经验NT.AL.欧洲杯足球竞彩材料和设备2020欧洲杯下注官网氯化聚丙烯(CPP)是一种商用产品，氯含量为重量的30%，购自广东金珠江化工厂。CPP的粘度平均分子量为174000克/摩尔。甲苯是A.R.GRADE。 采用JY92-进行超声辐照II由宁波（中国）新智生物化控制有限公司制造的细胞粉碎机以其全强度的68％，为650名义上是20-25千赫。超声波探头，平坦表面直径为6mm，直接触点样品溶液。反应器是450Ml玻璃容器与护套保持温度恒定在200.C在声波降解法。样品溶液的体积为240毫升。在定义的超声处理时间之后，除去一部分样品溶液以测量其特性粘度[η]通过奥布布尔跳跃粘度判断。 实验研究方法改进如下: （1）在以前的文献中，聚合物的浓度通常低于5%（w / w）[5-8]。考虑到工业生产，我们将CPP的最大浓度设置为20%。 （2）超声波时间不超过400在之前的文献中[5，6，9，10，12]。为了详细探讨超声时间对分子量的影响，在我们的研究中，我们设定的最长时间是3120分钟。 我分子量的钝化[η]，按参考文献[13]计算。Mark-Houwink方程[14][η] = 0.0174.m0.6919应用以确定降解CPP的粘度平均分子量。 结果和讨论D含量的测定ATA拟合技术常用的聚合物超声降解动力学方程如下: Baramboim的等式[15-18]
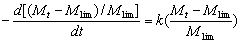（1）
在哪里m0.和mT.表示时间点的分子量0.和T.分别。mlim极限分子量是和吗K.表示超声降解的速率常数。 通过积分，式(1)可表示为: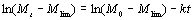 
（2）
（2）Ovenall的等式[5]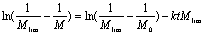 
（3）
自
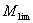和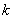
都是常量，根据Ref.[19]，它们可以合并为一个常量。 
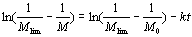（4）
（3）Giridhar Madras [7]建议基于理论推导的以下动力学方程：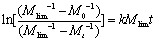 
（5）
可以证明方位。（5）与方程式一致。（3）通过检查计算。因此，方程式。（3）在本研究中使用。 (4) Malhotra的方程[3,9，16、20) 
（6）
为了确定动力学方程的表达式，我们首先需要确定其他参数m0.那m和T.。的参数K.式(6)中容易确定;当
和T.策划,K.式(3)中，由回归方程的斜率可得。但mlim和K.在方程。（2）和方程。（3）不易确定。原则上，获得mlim，实验必须长时间进行，直到分子量没有进一步变化。然而，这是不容易或实际进行很长一段时间。因此，根据不同研究者的经验，出现了以下经验方法:(1)秀元等将最终实验分子量视为极限分子量[15]。（2）Chakraborty等。发现了mlim在测量时，在120分钟后的分子量约为80％mlim在3H[2]。然后Chattopadhyay等人直接获得mlim使用该比例的聚（乙酸乙烯酯）和聚（氯乙烯）[7]。在该物品中替换动态方程mlim，实验数据的拟合更好。(3) Li等研究聚酰胺6[16]、高密度聚乙烯[17]、聚苯乙烯和三元乙丙橡胶[18]熔体聚合物的降解动力学时，选择式(2)作为这些聚合物的动力学模型。然后,mlim和K.根据动态模型获得，在替代后应该完全适合实验数据mlim和K.。 现在,mlim为动力学方程的参数，以便与最佳实验数据拟合，mlim应视为与K.通过数据拟合技术。如果动态方程是准确的，需要满足两个条件:一是动态方程对实验数据的拟合精度高;其次,mlim通过数据拟合技术获得应符合或接近经过长时间后获得的实验性分子量。如果数据拟合技术是可行的，实验不需要执行长时间才能获得mlim。这可以节省大量的调查时间。 我们采用并开发李的确定方法mlim和K.确定CPP在甲苯溶液中的动态方程。不同之处在于，通过比较许多动态方程的拟合精度而不是使用单个动态方程来找到最合适的动态方程，而不是使用单个动态方程，并且在本文中阐述了确定动态方程的特定过程。 的决心mlim和K.在动力学方程中在审查回归方程的准确性时的数据处理中y = f（x）用于拟合实验数据X，统计数据剩余标准偏差(S.E.)通常作为评价指标[21]。的计算公式S.E.是：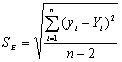
， 在哪里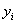
和y一世是实验值和计算值y在一世点,分别N为实验点的个数。该方法也可用于评价超声降解动力学方程拟合聚合物分子量的准确性。相应的表达S.E.超声降解为
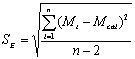， 在哪里m卡尔是理论价值mT.根据动力学方程计算。从表达S.E.,如果S.E.为零,m卡尔就等于mT.动力学方程将完全精确。当然，值越低S.E.那动力学方程的精度越高。 获得的步骤mlim和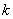
如下面所述： （1）估计价值mlim这小于最终实验分子量的那种，将在使用方程式的每个基准点处获得相应的速率系数。（2）或方程。（3）。这里的速率系数标记为K.一世。 （2）计算每个的平均值K.一世,标记为K.的价值K.在方程。（2）或方程式（3）。 （3）放置mlim和K.回式(2)或(3)计算每个基准点的分子量，计算结果为m卡尔。 （4）修改价值mlim和迭代(1)-（3）直到最小S.E.是实现。相应的mlim和K.是最优值吗mlim和K.式(2)或式(3)中。 (5)S.E.采用不同的动力学方程进行计算，比较实验数据的拟合精度。 需要注意的是，由于CPP在降解前的分子量大于170000G /molS.E.比1高很多。 CPP的实验结果在不同浓度下研究了CPP的超声波降解。温度保持在200.C超声过程中，超声强度设为440W。人们发现在各浓度下，CPP的粘均分子量随时间的增加而减小。在低浓度下，分子量的降低比在高浓度下更大。表1中列出的实验数据清楚地显示了这些结果。 常见动力学方程的CPP数据处理结果首先，使用公式(2)对表1所列的实验数据进行处理。结果发现，除20%的数据集外，拟合精度较低。即，误差之间公式(2)中包含理论和实验值。结果如图1所示。价值S.E.使用公式(2)列于表2。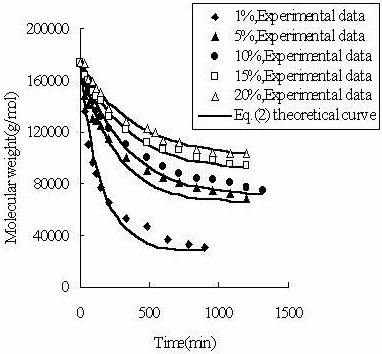 
图1。公式(2)与所测CPP分子量的拟合。 表1。不同浓度（g / mol）的CPP的粘度平均分子量。
|
0. |
174000 |
174000 |
174000 |
174000 |
174000 |
30. |
136000 |
148000. |
158000 |
164000 |
173000. |
60. |
111000 |
141000 |
150000 |
160000 |
161000 |
90. |
97000 |
130000 |
143000. |
152000 |
159000 |
120 |
88000. |
129000 |
137000. |
147000 |
153000 |
150 |
81000 |
125000 |
132000. |
144000 |
151000 |
210 |
66000. |
114000 |
123000 |
133000. |
139000. |
330 |
53000 |
100000 |
111000 |
122000 |
128000 |
480 |
47000 |
91000. |
100000 |
112000. |
123000 |
540 |
- |
- |
- |
- |
120000 |
600 |
- |
86000 |
94000 |
107000. |
113000 |
630. |
37000 |
- |
- |
- |
- |
720. |
- |
81000 |
88000. |
106000 |
111000 |
780 |
33200 |
- |
- |
- |
- |
840. |
- |
77000. |
84000 |
101000. |
107000. |
900 |
30300. |
- |
- |
- |
- |
960. |
- |
75000 |
83000 |
98000 |
105000 |
1080. |
- |
72000 |
81000 |
96000 |
104000 |
1200 |
- |
69000 |
77000. |
94000 |
103000 |
1320 |
- |
- |
75000 |
- |
- |
3120. |
18000. |
- |
- |
- |
- |
表2。不同动力学方程的CPP数据处理结果。
|
1％ |
17000. |
6.79×10－8 |
10246 |
2944 |
7360 |
1866年 |
５％ |
56000. |
4.91×10－8 |
8119. |
5869. |
16806. |
4096 |
10％ |
57500 |
3.42×10－8 |
6262 |
2695 |
13816. |
1925 |
15％ |
73000. |
3.14×10－8 |
3130. |
1565 |
12948 |
1449 |
20％ |
75000 |
2.25×10－8 |
2426. |
2634 |
8489. |
2824 |
然后，EQ（3）和EQ。（6）用于处理CPP的实验数据。但结果也不尽人意。价值S.E.使用Eq.(3)和Eq.(6)也在表2中列出。 一个电子战动力学方程如果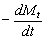
定义为超声降解速率，式(2)可表示为 
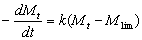（7）
eq。（6）可以表示为：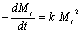 
（8）
如果eq。（7）与方程式相结合。（8）和期限mlim式(6)中，我们提出一个新的二阶动力学方程: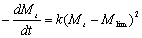 
（9）
通过集成，eq。（9）可以表示为： 
（10）
根据最小值的原则S.E.，EQ。（10）用于符合表1中列出的实验数据。如图2所示，等式描述了表2中列出的实验数据。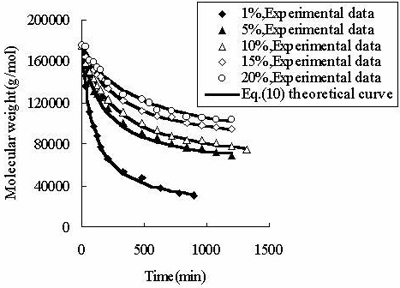 
图2。公式(10)与所测CPP分子量的拟合。 在表2中，对于CPP浓度为1%〜15％，结果S.E.计算使用eq。（10）是最低的在所有S.E.。等式的拟合精度。（10）高于其他方程。虽然价值S.E.在20％的浓度下不是最低的，它接近最低值，并且等式的相关系数。（10）在20％浓度下为0.99，其足够高，以证明其准确性。 为了验证是否是理论值mlimEq.(10)预测正确，超声降解在1%浓度下进行了很长时间。不出所料，这是实验性的mlim18000克/摩尔(表1)和理论mlim是17000G / Mol.(表2）。在此基础上，如果超声时间也延长5%〜20％的浓度，理论值mlim也是必然得到的。因此，超声波降解甲苯溶液中的CPP obeys新的二阶动力学方程-情商,(10)。 上述结果证明mlim和K.可以通过数据拟合技术得到。 方程式的一般适用性分析。（10）为了调查一般意义eq。(10)，用于拟合从文献中收集的原始数据。结果列出了桌子3.结果表明，该方法的精度较高eq。(10)比现有文献中的动力学方程高。 价值S.E.证明eq。（10）描述了一些聚合物的动力学行为而不是文献中的动力学方程。因此，eq。(10)是对传统的超声辐照下聚合物动力学方程的一个新的补充。 表3。相对比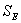
之间eq。（10）文献中的动力学方程。
|
1 |
环己基（溶剂：甲苯） |
12720. |
5968 |
85000. |
2 |
异丁基（溶剂：甲苯） |
4961 |
4764 |
30000 |
3. |
己(溶剂:甲苯) |
12283 |
9865 |
45000. |
4. |
十六烷基（溶剂：甲苯） |
8753 |
3614 |
100000 |
5. |
正丁基（溶剂：甲苯） |
12031 |
2682 |
49000 |
6. |
异丙基(溶剂:甲苯) |
26329 |
4345. |
65000. |
7. |
异十癸基（溶剂：甲苯） |
14016 |
719. |
65000. |
8. |
十二烷基(溶剂:甲苯) |
16958 |
3745 |
130000 |
9. |
十八烷基（溶剂：甲苯） |
47657 |
6405 |
135000. |
10 |
乙基（溶剂：THF） |
6246 |
6237 |
5000 |
11 |
正丁基(溶剂:四氢呋喃) |
2963 |
2476. |
20000 |
12 |
异丁基（溶剂：THF） |
6665 |
5115 |
50000 |
13 |
异癸(溶剂:四氢呋喃) |
15706 |
7521 |
50000 |
14 |
月脲（溶剂：THF） |
12729 |
9630 |
60000 |
15 |
异丙基(溶剂:四氢呋喃) |
30900 |
6654 |
60000 |
16 |
十六烷基(溶剂:四氢呋喃) |
9058 |
1076. |
80000 |
17 |
十八烷基（溶剂：THF） |
31566 |
7391. |
80000 |
18 |
壳聚糖0.2％0°C |
20436. |
18956 |
17000. |
19 |
壳聚糖0.8％0°C |
60916 |
57873 |
50000 |
20. |
壳聚糖1.4％5.0°C |
78806 |
77459 |
84000 |
21 |
Polystyrene-L257 |
29146. |
15221 |
70000 |
22 |
Polystyrene-St8 45.5/364 |
23544. |
14123 |
31000 |
关系之间的关系K.如:lim和CPP的浓度如表2所示，K.随CPP浓度的增加而降低mlim随浓度的增加而增加。这与文献报道的关系一致[5，6，9，22]。减少K.说明超声降解速率变慢，增加mlim说明超声降解程度较低。这表明超声波降解程度在更稀释的溶液中更加明显。这归因于浓度增加的链之间更强烈的缠结。这种纠缠抑制了溶剂和聚合物之间的能量转移[6，10]。这将导致空化气泡变得越来越小坍塌气泡周围的速度梯度较低在较高的浓度下。因此,退化效率随着浓度的增加而降低[9，23)。 结论（1）mlim超声波照射下的聚合物可以通过数据拟合技术得到。事实证明，该方法是可行的，通过该方法获得的结果是合理的。 (2)超声降解氯化聚丙烯在甲苯溶液中的动力学方程为: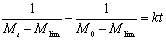 
(3)利用本文提出的新动力学方程，对文献中一些实验数据的拟合精度高于文献中动力学方程的拟合精度。我们的新方程可以很好地描述动力学行为一些聚合物。该方程是对传统的超声辐照聚合物动力学方程的一个新的补充。 (4)超声降解CPP在甲苯溶液中的速率系数随浓度的增加而减小和mlim随浓度的增加而增加。超声劣化程度在更稀释的溶液中更加明显。 参考文献1.R.S.枫树，下午瓜加尔纳，D.L.。Gobbi和D. Samio，“使用碘酸 - 溶剂和温度效应的1,4-CIS-聚异戊二烯的SOOOCHEMICAL降解”，欧洲聚合物杂志，33（2001）399-402。 2.Jayanta Chakraborty，Jayashri Sarkar，Ravi Kumar和Giridhar Madras，“超声波降解聚丁二烯和全同立构聚丙烯”，聚合物降解和稳定性，85（2004）555-558。 3.陈志强，“分子链结构对大分子机械化学降解的影响”，生物化学学报。方法，56(2003)117-139。 4.范仲磊，唐思业，刘大壮，朱东生，“氯化聚丙烯的研究进展”，中国现代化工，12(2004)16-19。 5.杨木和，“超声波降解聚丙烯酰胺溶液的研究”，高分子材料科学与工程，22(2003)129-131。 6.Min Larng Tsaih，Lan Zang Tseng和Rong Huei Chen，用超滤处理去除小片段的影响和超声状况对壳聚糖的降解动力学“，聚合物降解和稳定性，86（2004）25-32。 7。Sujay Chattopadhyay和Giridhar Madras，“温度对聚（乙酸乙烯酯）和聚（氯乙烯）超声降解的影响”，应用聚合物科学杂志，88（2003）2818-2822。欧洲杯线上买球 8。T. Miyazaki，C. Yomota和S.Okada，“透明质酸超声波解聚”，聚合物降解和稳定性，74（2001）77-85。 9。Mohammad Taghi Taghizadeh和Abbas Mehrdad，“用粘度法计算聚乙烯醇水溶液的超声降解速率常数”，超声波与声学化学，10(2003)309-313。 10.Farah Kanwal，John J.Liggat和Richard A. Pethrick，“聚苯乙烯溶液的超声波降解”，聚合物降解和稳定性，68（2000）445-449。 11.A. Gronroos, P. Pirkonen和O. Ruppert，“超声解聚水溶性羧甲基纤维素”，声学化学，11(2004)9-12。 12.周晓东，林群芳，傣族，姬比亮，“多晶硅聚合物超声降解”，聚合物降解和稳定性，60（1998）409-413。 13.何曼军，陈伟晓，董西霞，“聚合物的分子量”，高分子物理，上海(1990)，pp.174-180。 14.大卓刘，中秀粉，培勤太阳和徐先生，“氯化聚丙烯和马来酸酐接枝氯化聚丙烯的溶液性能”，物理学和化学液体，42（2004）551-560。 15.倪秀源，胡跃芳，刘百林和徐曦，“羟乙基纤维素的机械降解和机械化学共聚”，欧洲聚合物杂志，37（2001）201-206。 16.李江，梁梅，郭少云，林颖，“超声辐照下聚酰胺6熔体的断裂和延伸研究”，高分子材料的降解与稳定性，18(2004)233 -329。 17。李云涛，李江，郭少云，李慧林，“超声辐照下高密度聚乙烯熔体的机械化学降解动力学及机理”，声学化学，12(2005)183-189。 18。李江，郭少云，李晓南，“超声辐照下聚苯乙烯和三元乙丙橡胶熔体的降解动力学”，高分子材料的降解与稳定性，89(2005)6-14。 19。何广波，陈克强和徐曦，“聚（氯乙烯）与丙烯酸丁酯的超声降解和共聚（氯乙烯）”，11（1995）56-61。 20.J.P. Lorimer和T.J.梅森，“Coventry大学Sonochemistry中心最近的一些研究”，超声波Sonochemistry，2（1995）81-86。 21.孙培勤，刘大壮，“线性回归”，实验设计，数据处理与计算机仿真，郑州，(2001)pp。44. 22.Giridhar Madras和Sujay Chattophadhyay，“苯甲酰过氧化物对聚（乙酸乙烯酯）的超声降解的影响”，聚合物降解和稳定性，73（2001）33-38。 23.答:Gronroos。P. Pirkonen, J. Heikkinen, J. Ihalainen, H. Mursunen和H. Sekki，“水溶液聚乙烯醇的超声解聚”，超声声学化学，8(2001)259-264。 联系方式唐思业，刘大庄 化学工程学院
郑州大学
郑州450002 电子邮件：[电子邮件受保护] |