2018年12月10
晶体中的原子通常形成有序的晶格。这样的结晶固体对轻微的变形会产生弹性反应:在去除施加的应变后,宏观的应力,以及原子晶格的微观结构,都会恢复到原来的状态。
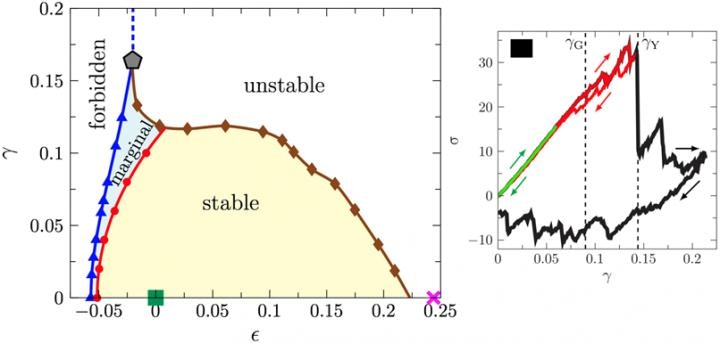 左:硬球非晶固体的稳定性-可逆性图,以体积和剪切应变表示。右图:典型的应力-应变曲线,显示可逆(绿色)和部分可逆(红色)行为。(图片来源:金玉良)
左:硬球非晶固体的稳定性-可逆性图,以体积和剪切应变表示。右图:典型的应力-应变曲线,显示可逆(绿色)和部分可逆(红色)行为。(图片来源:金玉良)
相反,如果一种材料不能回到它的初始状态,它就表现出塑性。一般来说,只有当变形足够大时,才会产生塑性。
为了解决这个问题,中国科学院理论物理研究所(ITP)的金玉良博士中国科学院欧洲杯线上买球,他和他的合作者使用了一个数值模型系统来彻底分析非晶态固体的力学特性。
微观结构可能是不可逆的,而宏观性质,如应变和应力,是可逆的,当一个小的变形被释放。在摄动前和摄动后构型之间转换所需要的功是不重要的。这种类型的非晶固体被称为“边缘稳定”,是由加德纳跃迁引起的,这是最近平均场理论所预测的。
科学家们进一步建立了硬球非晶固体的稳定性-可逆性图。这张图统一了包括塑性、弹性、卡压和屈服在内的力学行为。
根据稳定性-可逆性图,非晶固体具有两种特性,这两种特性取决于体积应变和剪切应变水平。在稳定区域的非晶固体实际上是可逆的和弹性的,类似于晶体。另一方面,在边缘稳定区域,弹性和塑性不可避免地结合在一起,即使是非常小的变形。此外,一种稳定的无定形固体只是部分可逆的。
研究表明,需要一种更完整的弹性理论——一种能够精确地整合非晶固体的理论。它还提供了一个重要的理解复杂的机械材料的设计,如金属玻璃。欧洲杯足球竞彩
研究合作者包括日本大阪大学的吉野Hajime博士;Université Paris Saclay的Pierfrancesco Urbani博士,法国;以及法国École Normale Supérieure的Francesco Zamponi博士。